Trystan Lea

Thermal Mass 1

Published: 2nd June, 2018

Another attribute that effects space heating and one I've wanted to explore in more detail is thermal mass . We experience the effect of thermal mass or the thermal capacity of materials when we have to wait for a room to heat up after switching the heating on, or feel it cool down over night.

Thermal mass is usually thought of in relation to absorbing solar gains, an insulated concrete slab floor, or rammed earth walls under direct sunlight can absorb the heat from the sun through the day and then release this heat through the evening resulting in a more stable indoor temperature as well as reducing heating and cooling demand.

Another perhaps less discussed potential use of thermal mass that is particularly applicable to more northern climates where the summer cooling load is relatively small but the winter heating load is high - and especially windy countries such as the UK, could be to use building thermal mass as a large thermal battery to absorb excess wind energy at times of low electricity demand in order to then reduce peak time electricity demand that would likely result form a large shift to electrified heating.

Esmond Tresidder discusses the idea in his paper "Scottish Passive Houses as wind - energy buffers"

This screenshot shows the effect of a 2.0 kW electric heater in our living room turned on at 8:30am running until about 12am before being turned down to the second heat setting (~1.2 kW) until about 6:30pm:

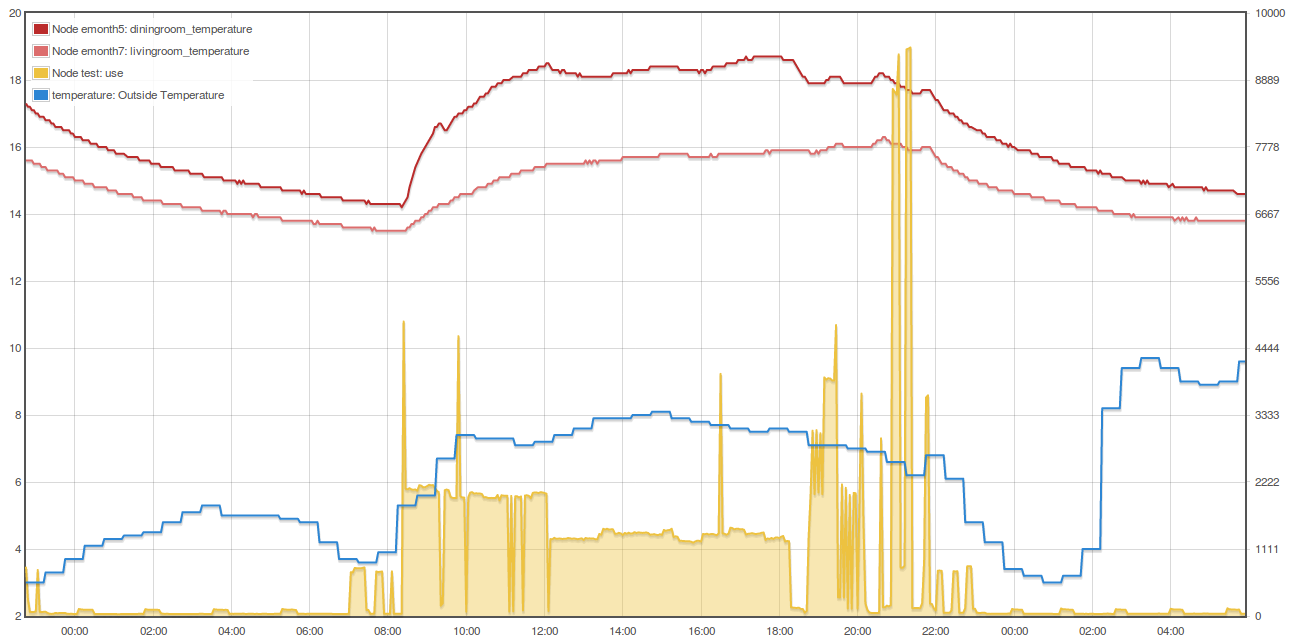
The dining room took 2h40 and about 5.3 kWh to raise the temperature from 14.3C to 18.0C. The night before it took 10h15 to drop from 18.0C to 14.3C.

A number of years ago now I did some work developing a dynamic simulation of thermal mass in a simple building that showed promise. I was able to simulate the internal temperature from a measured heat input data and the external temperature. But I did not manage to build on this model for more complex buildings, or fully relate the model parameters to the physical materials of the building, rather they where found by a process of trial and error until the simulated temperature provided a good match.

You can read my enthused posts from the time here:

How much thermal mass is there in our house? How much is there in external walls, party walls, internal walls, floors, furniture etc.

To try and answer this question I'm going to start by compiling a summary of the different elements in the house and their volume and then look at suitable thermal capacities for each of these elements.

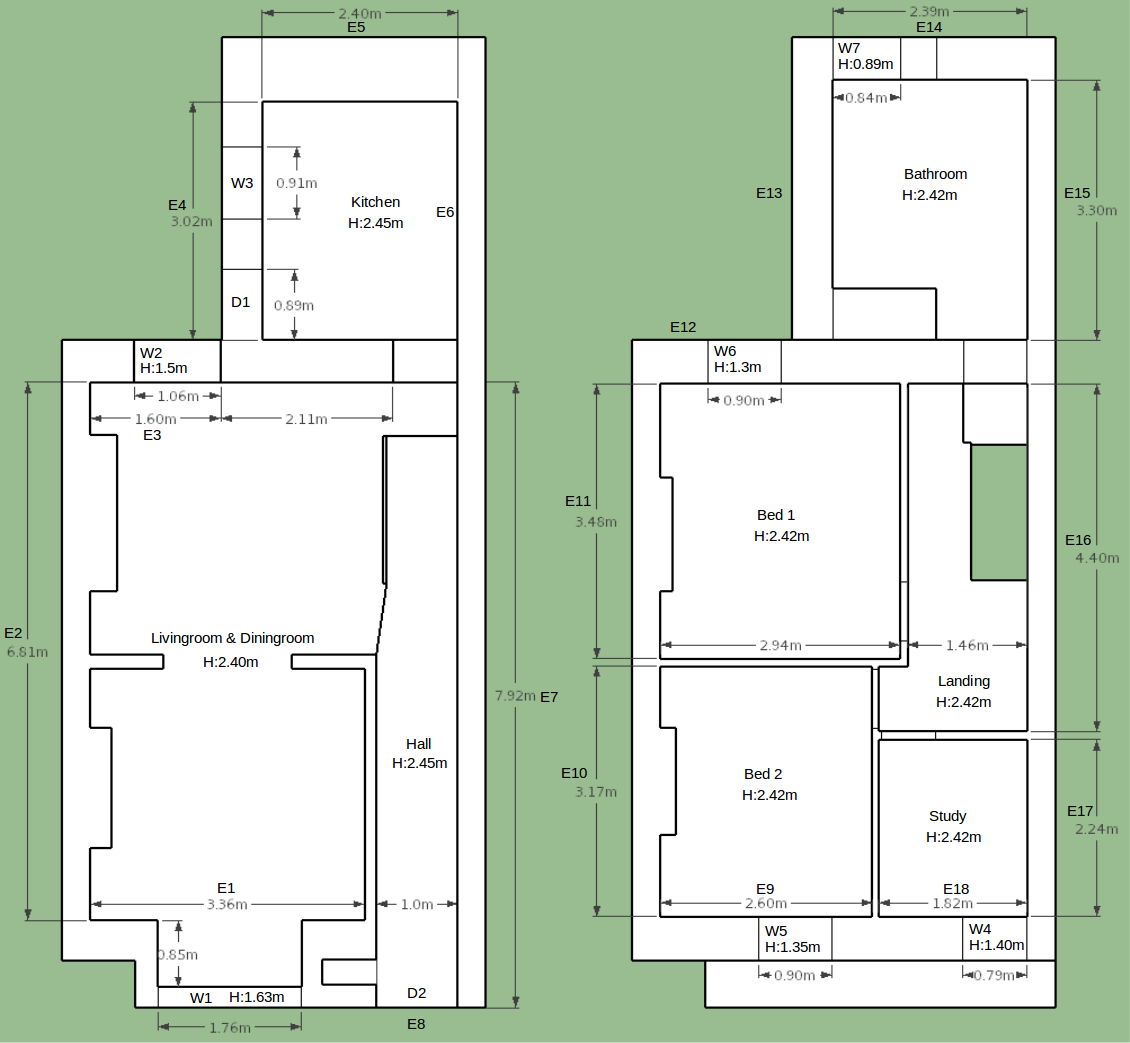
External Walls: Looking again at the floor plan for the house the volume of the south facing external wall is slightly complicated by the dormer window like feature on the ground floor of the house. To simplify the calculation Im going to remove this feature and assume a straight wall with the volumes of the openings subtracted. The full width of the front of the house is 5.2m including the parts of the wall that overlap the party walls on both sides. The full height of the external wall is 5.1m, resulting in an external surface area of 26.52 m2.

Subtracting out of this the area of the livingroom window (2.87m2), the front doorway (2.45m2), the window in bedroom 2 (1.22m2) and the window in the study (1.11m2) results in a net area of 18.87 m2. Multiplying the net area by the wall thickness of 0.5m gives a volume of 9.44m3.

The first section of the back wall bordering the livingroom is 1.96m wide, 5.1m high and 0.5m thick and has two windows of area 1.59m2 and 1.17m2 resulting in a total volume of 3.62m3. The west facing kitchen wall is 3.02m long with a door 2.12m2, window 1.15m2 and total volume of 6.07 m3. The north facing kitchen wall is 3.24m wide with one window 0.75m2, giving a volume of 7.89 m3. The total volume of both the front and back external wall is therefore 27.02 m3.

The external walls are stone construction with cement mortar. Looking up the thermal capacity of granite and cement mortar I found the following values:

Granite:             790 J/kg/K   2650 kg/m3
Cement mortar:       837 J/kg/K   1858 kg/m3
Air:                1005 J/kg/K   1.25 kg/m3

If the wall was made up of 100% Granite:

1.0m3 of granite x 2650 kg/m3 = 2650 kg x 790 J/kg/K = 2094 kJ/K.m3

70% Granite, 30% mortar:

0.7m3 of granite = 1855 kg, 1465 kJ/K.m3
0.3m3 of mortar =   557 kg,  466 kJ/K.m3
Total:                      1931 kJ/K.m3

70% Granite, 25% mortar, 10% air:

0.70m3 of granite =  1855 kg,   1465 kJ/K.m3
0.20m3 of mortar  =   372 kg,    311 kJ/K.m3
0.10m3 of air     = 0.125 kg,  0.126 kJ/K.m3
Total:                          1776 kJ/K.m3

As a starting point I will use the 70/20/10 value of 1776 kJ/K.m3. Multiplying this by our approximate wall volume we get:

27.02 m3 x 1776 kJ/K.m3 = 47,988 kJ/K (13.3 kWh/K)

It's then interesting to look at how much energy it would take to bring this wall to a steady state where there is a linear temperature profile between say 10C on the outside surface and 20C on the inside surface. At an average of 5C above the external temperature, the wall would take 13.3 kWh/K x 5K = 66.6 kWh to heat up! That's a fair bit of energy and about 2.5x the average daily heating demand.

Party Walls:
The west facing party wall is 6.81m long, 5.1m high and I will assume a thickness of 0.5m, giving a volume of 17.37 m3. The east facing party wall is 12.3m long, giving a volume of 31.36 m3. The total party wall volume is therefore 48.73 m3. The party walls are of a similar construction to the external walls and so assuming a similar thermal capacity, the total thermal capacity of the party walls adds up to:

48.73 m3 x 1776 kJ/K.m3 = 86,544 kJ/K (24.0 kWh/K)

Assuming that both sides of a party wall are heated to 20C and to simplify things that there is no temperature gradient on the edges, heating up the walls from 10C would take 240 kWh.

Internal Walls:
The internal walls are comprised of one segment of stone wall between the kitchen and livingroom, measuring: 2.11m x 0.5m x 5.1m = 5.38 m3, with a thermal capacity of:

5.38 m3 x 1776 kJ/K.m3 = 9,555 kJ/K (2.7 kWh/K)

Contributing 27 kWh to our total 10C to 20C heat-up energy.

Then there is a number of stud frame and plaster board walls 3.78m downstairs and 11.33m including doors upstairs, A total length of 15.11m.

Assuming 400mm spacing with 2x4 studs (of actual dimentions 38mm x 89mm). 15.11m would require around 38 studs. Lets say the wall height is 2.4m subtracting 38mm top and bottom 'plates', would leave a stud height of 2.32m.

Studs: 0.038m x 0.089m x 2.32m x 38 = 0.30 m3
Bottom and top: 0.038m x 0.089m x 15.11m x 2 = 0.10 m3

The density and thermal capacity of pine is around 470 kg/m3 and 1650 J/kg/K respectively and so the thermal capacity of the stud frame is:

0.4m3 x 470 kg/m3 = 188 kg x 1650 J/kg/K = 310 kJ/K (0.086 kWh/K)

The density and thermal capacity of plasterboard is around 950 kg/m3 and 840 J/kg/K respectively assuming a 10mm thickness and 2.4m height two sides of 15.11m results in a volume and then thermal capacity of:

0.010m x 2.4m x 15.11m x 2 = 0.73 m3
0.73 m3 x 950 kg/m3 = 693.5 kg x 840 J/kg/K = 583 kJ/K (0.162 kWh/K)

Our stud frame internal walls therefore only add about 0.25 kWh/K. Given that all of this is internal it would contribute 2.5 kWh to heat from 10C to 20C.

Its likely that the 1st floor adds a similar amount, lets say 4 kWh to take into account thicker construction. The loft has a temperature gradiant across is and so we would expect a smaller amount of heat storage perhaps similar to our walls at 2.5 kWh.

Ground floor:

There are two parts to the ground floor:

24.4m2 of hardwood flooring, insulated above the concrete slab
15.2m2 of solid tiled ground floor on top of the concrete slab

The hardwood timber floor is 20mm thick, multiplied by 24.4m2 equates to 0.488 m3 of timber.

20 mm x 24.4 m2 = 0.488 m3, x 700 kg/m3 = 341.6 kg, x 1600 J/kg/K = 546 kJ/K (0.15 kWh/K)
0.15 kWh/K x 10K = 1.5 kWh

Assuming a 100mm thick cast concrete slab with a density of 2000 kg/m3 and heat capacity of 1000 J/kg/m3:

100 mm x 15.2 m2 = 1.52 m3, x 2000 kg/m3 = 3040 kg, x 1000 J/kg/K = 3040 kJ/K (0.84 kWh/K)

There is a temperature gradiant across the solid ground floor which halves the heat stored at our 20C steady state to 4.2 kWh.

Air volume: Total volume of air from MyHomeEnergyPlanner assessment 185 m3

185 m3 x 1.25 kg/m3 = 231 kg x 1005 J/kg/K = 232 kJ/K (0.064 kWh/K)

Total Energy Stored heating from 10C to 20C

Adding up all the different elements:

66.6 + 240 + 27 + 2.5 + 4.0 + 2.5 + 1.5 + 4.2 + 0.6 = 348.9 kWh

The MyHomeEnergyPlanner model suggests the heating demand of the house to be on average 26.6 kWh per day. The total heat stored at steady state with an internal temperature of 20C and outside temperature of 10C is therefore around 13 days!

Specific heat, thermal capacity of different materials:

Timber, Larch:                   1400 J/kg/K
Timber, pitchpine:               1300 J/kg/K
Timber, pine:        470 kg/m3   1650 J/kg/K
Timber, oak:                     2400 J/kg/K
Timber (various):    500 kg/m3   1600 J/kg/K   0.13 W/m/K   CIBSE guide A 2006
Hardwood             700 kg/m3   1600 J/kg/K   0.18 W/m/K   CIBSE guide A 2006

Granite:            2650 kg/m3    790 J/kg/K
Slate:              2691 kg/m3    760 J/kg/K
Limestone:                        909 J/kg/K
Sandstone:          2300 kg/m3   1000 J/kg/K   1.80 W/m/K   CIBSE guide A 2006
Cast concrete       2000 kg/m3   1000 J/kg/K   1.33 W/m/K   CIBSE guide A 2006
Screed              1200 kg/m3   1000 J/kg/K   0.46 W/m/K   CIBSE guide A 2006

Lime,sand render    1600 kg/m3   1000 J/kg/K   0.80 W/m/K   CIBSE guide A 2006
Cement,sand render  1800 kg/m3   1000 J/kg/K   1.00 W/m/K   CIBSE guide A 2006
Dense Plaster       1300 kg/m3   1000 J/kg/K   0.57 W/m/K   CIBSE guide A 2006
Lightweight Plaster  600 kg/m3   1000 J/kg/K   0.18 W/m/K   CIBSE guide A 2006
Plasterboard         700 kg/m3   1000 J/kg/K   0.21 W/m/K   CIBSE guide A 2006
Cement mortar:      1858 kg/m3    837 J/kg/K

Soil                1500 kg/m3   1800 J/kg/K   1.50 W/m/K   CIBSE guide A 2006
Air                 1.25 kg/m3   1005 J/kg/K